Home

Core Lecture 4a Policy Gradients and Actor Critic -- Pieter Abbeel

Reinforcement Learning is interesting!

November 12, 2021 LiJR lapinji

终于到Policy Gradient方法了！

一、引言

reinforcement learning研究的是智能体agent与环境environment进行交互，在交互的过程中学习的问题，RL的根本目的是进行策略的优化，希望最终能够获得最优秀的策略。策略（policy）指的就是一个函数，输入一个当前状态state，输出一个动作action（的分布），相当于给agent指明了一条路线，告诉agent在这个状态下应该如何行动，是一个路线图一样的存在。自reinforcement learning建立以来，人们尝试了多种方法希望求得这个最优policy，对这些方法及方法之间的关系进行大致的分类，结果如下图所示。

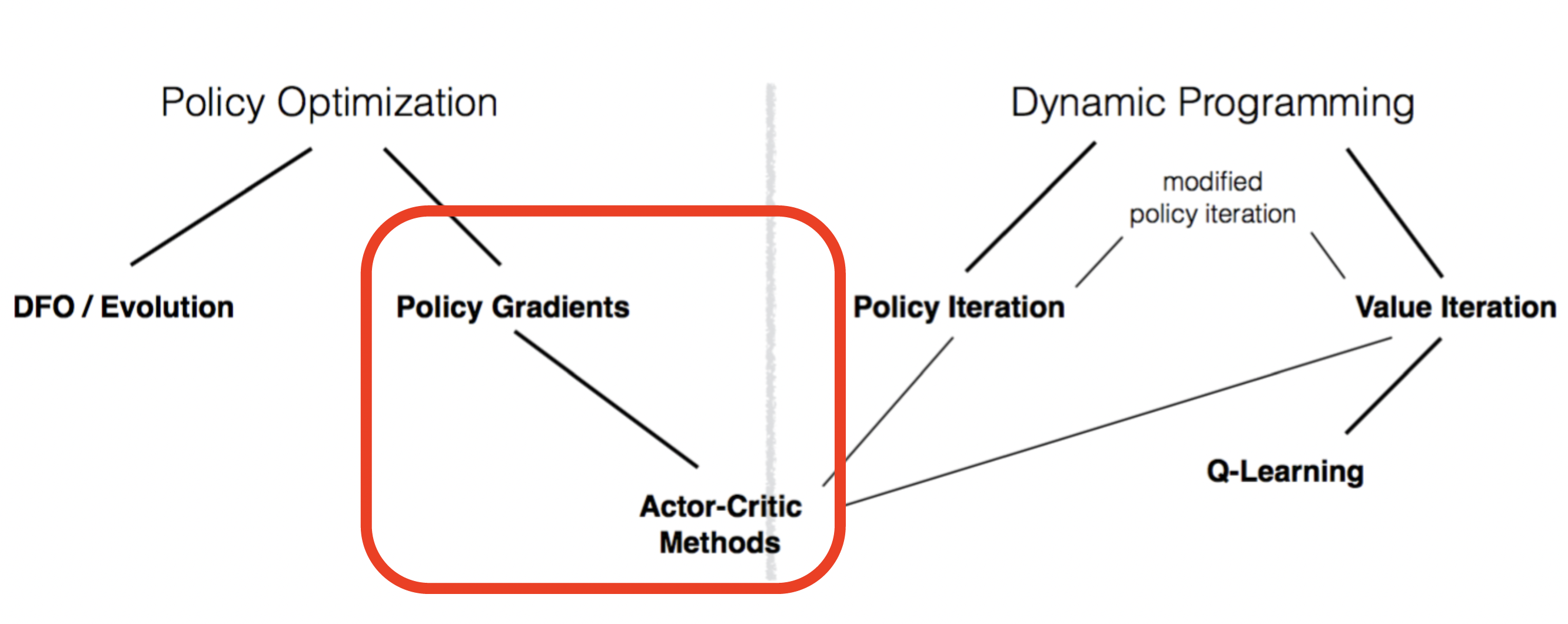
可以看到我们之前讨论过的方法基本都属于Dynamic Programming（动态规划）范畴，通过不断的迭代从简单想复杂推进，直至满足Q、V自洽方程组，Lecture 1中提到了Value Iteration方法（主要是state value）以及policy iteration方法，前者是通过对整个空间进行充分的探索，当对整个空间充分了解以后，策略就退化成了简单的greedy方法；后者则是一个不太一样的思路，着眼于policy的本质（给定状态进行动作选择），先对policy进行评估，获得遵循该policy全空间的value function，之后再根据评估的结果按照贪心的原则对policy进行修正，直到收敛为止。以上讨论的这两个方法的操作都是较为初级的，在之后我们详细讨论了value iteration中的Q-Learning方法，相比于state iteration方法，Q-Learning的策略更加明显，不需要采用argmax，可以直接取max值选择。在模型未知（model free）的情况下Q-Learning可以采用sample的方法，结合TD方法进行学习，每次设定一个target，以一定的学习率像其逼近。Q-Learning又有一系列变式，从记录所有状态-动作组合的Tabular Q-Learning到参数化的approximate Q-learning，再到终极形态DQN，以及对DQN存在的一些缺点的改进型（DDQN，Dueling DQN等），这些方法在dynamic programming的基础上建立起了复杂的RL算法系统，但是这些方法的根本想法是类似的，都是试图又简单到复杂（从随机初始化不断优化更新）最终获得关于全空间的价值信息。在获得了这些信息之后，agent每走到一个状态state，就会根据已知的环境信息看一下接下来的动作（到达的状态）的价值几何，之后简单地选择一个价值最高的action去执行。这样的方法看起来已经足够简单，但是实际上还是绕了个弯。在dynamic programming方法中我们主要的着眼点是环境，一直在力图通过建立value function的方法对环境信息有清楚明白的认知，至于策略嘛，在执行的过程中再看一下环境就知道了。但是Reinforcement Learning的最终目标是什么？并不是完整的环境信息，而是一个优秀的policy。优化policy才是我们的最终目标。与Dynamic Programming方法不同，Policy Optimization方法直接着眼于优化policy，从而开辟了一个新天地。

二、Policy Optimization概述

首先我们讨论一下什么是policy。policy是RL中agent的核心，接收环境提供的状态s，输出一个action给到环境。具体来说，policy接受state的输入，输出一个action的分布。我们使用神经网络对policy进行建模，policy的参数就是网络的权重。我们的目标是获得一个最优秀的policy，在这种定义情况之下指的就是期望获得policy参数 $\theta$使得 $E[\sum_{t=0}^HR(s_t)|\pi_\theta]$ 取到最大值。为什么我们在这里定义policy输出的结果是action的分布而不是直接的一个action呢，主要目的是方便policy的优化，达到"policy smoothly change"的目的。

为什么要使用policy optimization方法？主要有如下的三个原因

• 有的时候策略 $\pi$比value function（Q、V）更加简单

  例如robotic grasp任务

• V价值函数不能直接规定action，需要在模型已知的情况下使用argmax函数进行计算

• Q价值函数虽然相比V价值函数求解动作更为方便，但是也需要遍历所有的动作，这对连续空间/高位动作空间情况提供了挑战

使用一张表格对Policy Optimization方法以及Dynamic Programming方法的优劣进行总结

三、Likelihood Ratio Policy Gradient

根据刚才对policy的定义，我们对policy的优化实际上是为了求得 $U(\theta)=E[\sum_{t=0}^HR(s_t)|\pi_\theta]$的最大值，我们定义 $\tau$表示轨迹（trajectory），即一个state-action序列 $s_0,u_0,s_1,u_1,···,s_H,u_h$， $U(\theta)$可以表示为

正如上边(1)式所表示的， $U(\theta)$表示对参数为 $\theta$ 的policy价值的评估，最右项表示针对该policy下不同trajectory分别计算，每个trajectory所能够获得的reward根据其出现的概率进行加权平均，最终获得的就是该policy对应的价值reward，也就是对该参数 $\theta$下policy的评估，我们对这个评估进行梯度下降处理，达到优化的目的。

接下来对(1)式进行梯度计算的数学推导

通过以上推导，我们就获得了利用采样方法对policy评估函数 $U(\theta)$求梯度的式子。以上方法是Policy Gradient的核心内容之一，令人惊讶的是，它不仅仅适用于一般的情况，在R不连续甚至未知的情况下，上(3)式仍然适用，对采样的要求也不严格，即便是采样空间是离散的路径集合，上式一样可以获得正确的结果。

由(3)式结合梯度下降的原理，我们可以进行定性分析。如果按照 $\hat g$进行梯度下降计算，计算后的policy相比计算前会有如下改变：

• $R(\tau^{(i)})$为正的trajectory出现的概率会增加（ $\log P(\tau^{(i)};\theta)$增加）
• $R(\tau^{(i)})$为负的trajectory出现的概率会降低（ $\log P(\tau^{(i)};\theta)$降低）

通过梯度下降更新，我们按照以上原则改变了原先policy中不同价值的路径出现的概率，从而达到对路径进行优化的目的，但是实际上并没有对路径进行改变。

如何计算(3)式呢？我们需要对其中 $\nabla_\theta \log P(\tau^{(i)};\theta)$项进行一些更深入的探讨

由上边的推导可以得到，只需要知道trajectory上每一步的策略就可以对policy参数 $\theta$进行梯度计算，并不需要知道环境的dynamics model。综上所述，我们获得了计算策略价值评估函数 $U(\theta)$的基于采样的估计方法。将最终获得的计算式重写如下

考虑根据以上计算出的梯度结果进行梯度下降优化计算。根据之前的论述，我们达到的效果是当tragectory $\tau^{(i)}$ 对应的reward大于零的时候其出现的可能性就会增加，但是这样的效果并不令人满意，因为在实际情况中我们可能会面对大多数采样获得的trajectory均满足reward大于零的情况，就会导致这些trajectory的概率均会上升。但是我们需要的实际上是希望reward较大的trajectory的概率上升，较小的即便是正的概率也要下降，因此需要设定一个baseline，以区分不同trajectory的“价值”。不妨把这个baseline设置为b，那么我们使用的梯度就应该是：

从数学上可以证明，引入与action选择（trajectory）无关的b项对梯度值的求解没有影响

在(5)式中我们用采样的方法计算出了policy价值评估函数的梯度值，之前通过将 $P(\tau;\theta)$项中的trajectory展开成状态-动作序列获得了良好的效果，接下来对R项进行类似的细化处理

正如以上计算过程，我们在使用 $\hat g$ 的用于梯度下降时候，粗略的说是根据每条trajectory的价值增减其出现的概率，实际上是对trajectory序列中每个状态-动作组合分别处理，如果这个序列的价值是正的，序列中的每个状态-动作组合都会收到相同的处理，也就是按照相同的幅度进行该状态下该动作出现的概率增加。实际上这样做是不合理的，不能对一个trajectory中所有的状态-动作组合都这样相同对待。很可能会出现虽然整个trajectory的价值是正的，但是其中某一部分的贡献很大，另外一部分虽然policy很差但是加在一起仍然是正的，这样笼统对待概率增减明显是不合适的。因此需要对reward一项进行具体分析。正如(7)式所列的那样，我们将reward项按照分配律和同一个trajectory中不同t的每个状态-动作项的梯度相乘，之后再求和得出该样本trajectory的价值估计，再对每个t值将reward函数写开，(7)式中past rewards项指的是这部分rewards是t时刻之前的状态-动作转移获得的rewards，与t时刻这一步动作选择的好坏没有关系，只有之后future rewards and baseline项才描述了此trajectory当前时刻的动作选择对未来造成的影响。future rewards and baseline项实际上能够准确描述当前状态当前动作的价值大小，根据这个价值的大小决定这个动作选的怎么样，在更新policy的时候应该对这个动作的概率增加还是减少。这里有一句重要的话需要强调一遍，future rewards项 $\sum_{k=t}^HR(s_k^{(i)},u_k^{(i)})$描述了当前状态选择这个当前动作的价值大小。 按照这样的思路， $\hat g$的表达式应该是下边这样的：

(8)式就是经典的Policy Gradient算法核心表达式，根据m次trajectory采样的结果计算了当前policy的梯度，用以对policy进行优化，之后重复这一过程，就可以得到满足要求的policy。值得注意的是，在这种表达式下baseline项b的含义也有所改变，之前其代表整个trajectory获得rewards的“平均值”或者是“标准”，但是在舍弃t时刻之前获得的奖励之后，b就变成了从当前时刻出发之后能够获得的奖励估计值。我们在这里将其写作 $s_t$的函数，在之后会有更加深远的意义。

在具体操作的时候会面临一个问题。如何选择baseline？这个问题相当关键，事实上PG算法很多的优化版本正式针对baseline选择这个问题进行的改进。我们引入baseline(6)式中的b项代表一个constant baseline，表示整个trajectory的rewards平均值，即 $E[R(\tau)]\approx\frac{1}{m}\sum_{i=1}^mR(\tau^{(i)})$ 。这是通常的办法，简单易行，事实上有研究者曾经对constant baseline的最有取值做过严谨的数学研究，得出过一个颇为复杂的表达式，不过由于constant baseline本身就有很强局限性，这里对这个最优表达式略去不谈。(8)式中使用的Time-dependent baseline是我们重点关注的对象，首先一个最简单的方法是设定

这种设置方法虽然简便，但是更多的将baseline认为是一个时间t的函数。这样的做法固然可取，但是在不同的trajectory中时间t时所处在的state不同，众所周知出发的state对之后能取得奖励的大小有着决定性的影响，这种影响比探索时间更加重要一些，并且由于时间限制H通常很大，将baseline设定成 $s_t$的函数更加合适。那现在 $b(s_t)$代表什么含义呢？其表示的含义是：从状态 $s_t$出发，所能够获得的奖励的平均值（期望） ，这个平均值是依赖当前策略 $\pi$的，也就是说含义是：从状态 $s_t$出发，遵循当前policy $\pi$所能够获得的奖励的平均值（期望） 。这个定义正符合Lecture 1中“策略 $\pi$下状态价值函数 $V^\pi(s_t)$ ”的定义。使用这样的状态价值函数就可以比较当前采样到的trajectory在t时刻的动作选择带来rewards和遵循当前policy能够获得的收获，如果当前这个动作选择能够带来更大的收获，就应当增加其出现的概率（注意本节中的policy给出的都是action的分布）。

如何计算 $V^\pi(s_t)$呢，我们首先介绍Monte-Carlo方法。考虑到本节中的 $V^\pi(s_t)$函数也是一个神经网络，设其网络参数为 $\phi$，首先进行随机初始化获得 $V^\pi_{\phi_0}(s_t)$ 。之后按照policy进行采样获得m个trajectory（Monte-Carlo），在进行policy更新之前首先计算 $V^\pi(s_t)$，Monte-Carlo法的更新方式如下：

这是一种完全类似于supervised learning的想法，具有很好的效果。介绍另一种方法，是我们之前比较熟悉的TD（时序差分）方法。TD方法利用Bellman Equation进行迭代，与Monte-Carlo方法直接采样获得m个完整的trajectory不同，TD方法则是走一步优化一次，优化更新的频率高于Monte-Carlo方法。Bellman Equation是：

我们根据这个式子进行迭代优化。

进行了这么多理论分析，左图是Vanilla Policy Gradient（最标准的普通PG算法）的流程。可以看到VPG算法遵循Monte-Carlo方法计算state-dependent baseline函数，之后再对 $\hat g$进行计算，再使用梯度下降法对策略进行优化，如此重复直到获得满意的策略。

回顾一下Likelihood Ratio PG Estimator，即

这里着重标出了A项。A项 $\sum_{k=t}^HR(s_k^{(i)},u_k^{(i)})$ 代表的含义是当前这个trajectory下t时刻之后获得的rewards总和。之所以要计算这个值，是为了和当前策略当前状态的价值函数 $V^\pi(s_t^{(i)})$ 比较大小，判定此trajectory下当前状态选择的动作选的怎么样，根据差的正负大小决定梯度更新是此状态此动作的出现概率是增大还是减小。既然是为了衡量此状态下此动作选择的价值，当前这个 $A=\sum_{k=t}^HR(s_k^{(i)},u_k^{(i)})$ 的结果与trajectory后边状态的动作选择也有很大的关系。设想一种情况，如果当前这个状态动作选取非常恰当效果很好，但是trajectory之后的状态下动作选取全是一团糟，就会导致 $\sum_{k=t}^HR(s_k^{(i)},u_k^{(i)})$ 项值很小，低于baseline的话还会导致现在这个明明很好的动作出现的概率被降低。A项存在的目的是衡量此时此状态此动作选择的怎么样，不应当受到之后如何演变的制约。换句话说，这时候的策略更新衡量标准和Lec1中介绍的policy iteration高度相似，都是试图对当前这个动作做出一点改变，想要知道对于现在的policy，仅仅是在当前这个状态采用这个动作，别的情况下都不变，这样的话policy的效果究竟改变的怎么样。和计算baseline类似，我们希望通过一个Q函数去描述此状态下此动作选择的价值。为了增强计算的稳定性，我们引入折扣因子和函数近似。首先引入折扣因子 $\gamma$

再通过引入函数 $V^\pi(s_t)$如下：

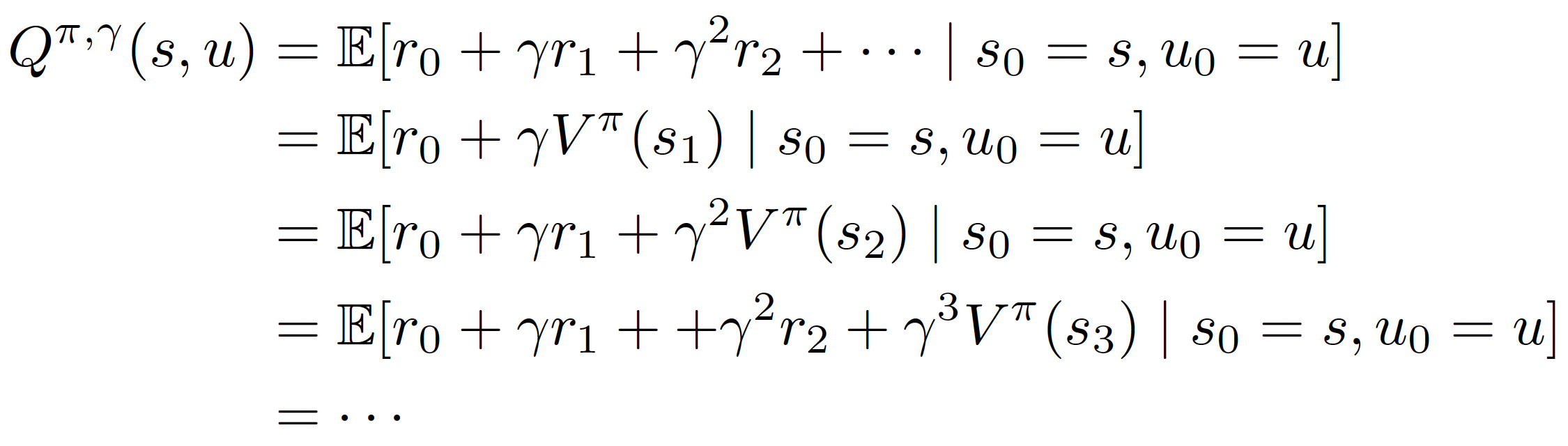
使用上边的折扣因子Q函数代替(9)式中的A项，就是著名的A3C(Asynchronous Advantage Actor-Critic)算法的核心思路。另外还有一个著名的算法也使用了类似的这种思路

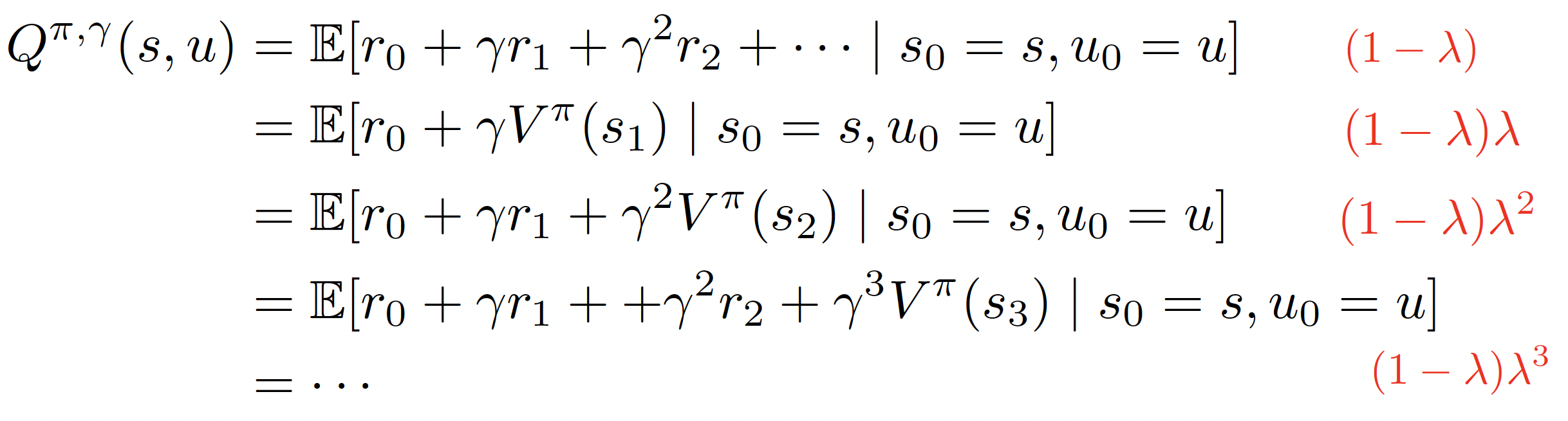
对以上的不同step采样估计的Q函数进行加权平均，权重如右侧红色字体所示，最终获得一个gereralized的Q函数带入进行PG计算，这种方法就是著名的GAE(Generalized Advantage Estimation)算法。A3C算法亦或是GAE算法，他们本质上都是Actor-Critic算法。有关Actor-Critic的内容之后也会涉及，这是RL中相当重要且前沿的一个部分。简单的说，Actor-Critic指的就是利用value function baseline的PG算法。在这里将GAE算法的大致流程列在下边，之后还会进行更详细的讨论。