Core Lecture 3 DQN + Variants -- Vlad Mnih

Reinforcement Learning is interesting!

LiJR lapinji

本讲讨论著名的DQN算法（Deep Q-Networks Algorithm）

一、对Q-Learning的简单复习

对于参数化后的Q函数 ，其自变量是当前所在的状态与进行的动作的组合，函数值代表这种组合对应的奖励值的大小。在进行学习迭代更新的时候采用逐步更新，逼近target的方式进行处理，其中target代表使用greedy方法，利用当前第k轮次Q函数确定的当前状态当前动作对应的奖励值的最优情况，我们引入学习率之后使用梯度方法逐步逼近target，用s‘给s赋值后重复这一过程。其中参数化的方式有很多种，其中一个特殊情况（ ）则退化成了Tabular Q-Learning，即用一张表格记录下所有可能的Q函数取值情况，这时每次更新只会对s，a对应的唯一参数产生影响，进行化简可以得到退化后的Tabular Q-Learning的迭代更新表达式。具体的过程如下图所示

QL_1

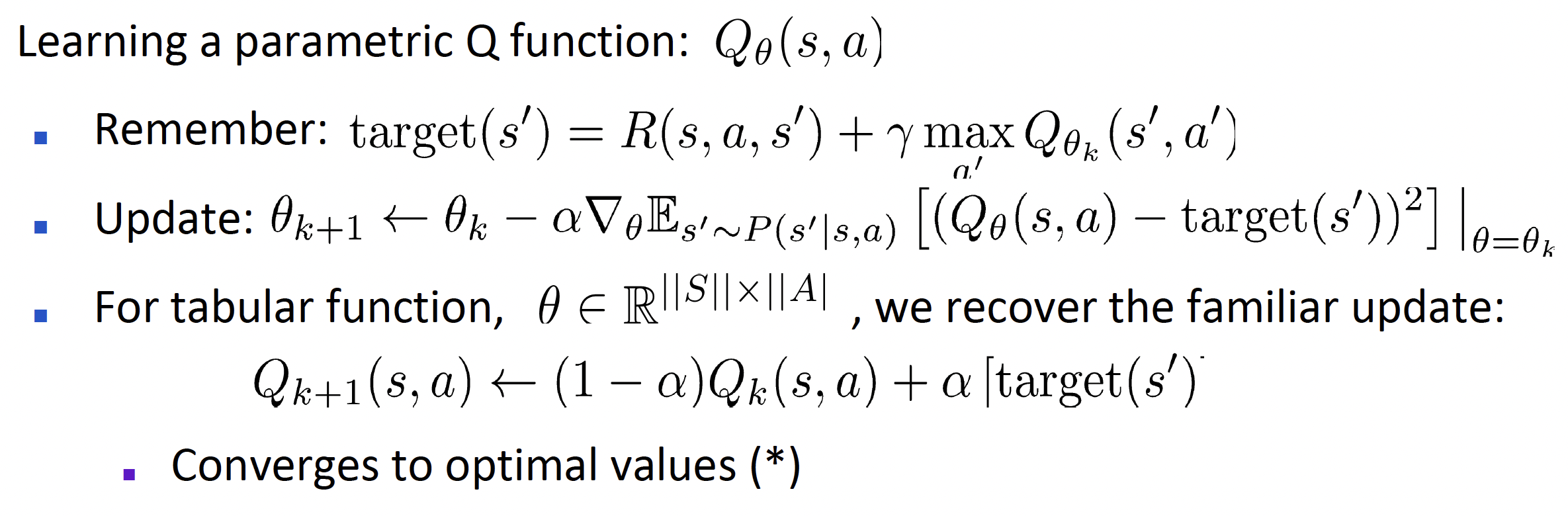
其中需要注意，对于tabular Q-Learning，每次更新Q函数之后相比于更新之前只对一个(s, a)组合的Q函数进行了改变，其他组合并没有发生变化；但是一般的Approximate Q-Learning中进行更新时虽然出发点是对一个特定(s, a)组合的Q值进行修正，但是由于参数化对状态进行了概括归纳(generalize)，这种改变同样会影响其他的状态-动作组合的Q函数值。本讲中我们着重考虑的情况是，由于参数化的方式十分多样难以选到合适的，不妨采用神经网络的方式对Q函数进行模拟，即确定一个Q-Network，输入是当前状态s与选择的动作a，输出是 ，参数即为网络的权重参数。但是DQN算法并不能简单地Approximate Q-Learning的方法中参数化的方式改成使用神经网络，参数是网络权重，这样会面临一些困难，在接下来的部分将会具体分析DQN针对这些问题的解决方法，也就是DQN的独特创新之处。

二、DQN算法

正如左图所示，直接用神经网络替换模拟函数主要会面临两个困难。第一个是不稳定性，正如上边所分析的那样，由于每次更新不仅会改变当前状态-动作组合的Q函数值，由于generalize的特点，同样也会改变其他状态-动作组合的Q函数值，因此一个现在已经“调好”的合适Q函数值也可能在对别的状态进行调整的时候再度被改变，离开已经处在的最优情况。另一个困难是更新和路径相关，或者说更新被限制在路径之内，这对整体的探索和学习来说并不是一件好的事情。

DQN算法的高层观点（High-level idea）是：使Q-Learning看起来更像supervised learning，为了提升稳定性，有两个关键的技术手段，一个是replay buffer，另一个是target network

（1）replay buffer

之前所描述的一般的Q-Learning采用online update的方法进行更新，也就是伴随着学习过程的进行，每走一步（state变化一次）就会对Q网络进行一次更新，但是这种更新过于频繁，是导致不稳定情况出现的原因之一。因此我们引入replay buffer来降低更新的频次。具体来说，我们把每次状态的transition pair（s, a, s', r）组合存入有一定容量限制的replay buffer中，随着探索的不断进行buffer中数据量的规模也在不断增大，在加入新的pair的时候也会讲旧的pair删除，最终将buffer中的数据量维持在一个合适的规模（一般是one million左右）。在学习更新Q网络的时候，对buffer中的pairs进行采样（比如采样32个pairs），之后就这32个pairs的情况进行学习，也就是分别求它们的Q函数值与各自的target方差（或者是别的误差函数），之后再求和，针对这个量进行梯度下降的更新操作。通过设置replay buffer有效降低了Q网络更新的频率，增强了学习的稳定性。

（2）target network

target network的设立是上述High-level idea的一个直接体现。在Q-Learning的过程中，我们通过梯度下降的方式让当前的Q函数（在当前状态-动作组合的Q函数值）趋近于target，以达到优化的目的，但是伴随着Q函数每次的更新，用于target计算的Q函数也随之变化，也就是计算target的“标准”也是一直在变化的，跟随Q函数的变化而变化。回顾一下target的计算过程，当不涉及terminal状态的时候，有

我们通过greedy的方式计算target值，这和我们在训练当中选择action的策略（最新Q网络， 策略）不同，即这种做法是off-policy的。这里之所以说target是s'的函数，是由于在给定s，a的时候，由于下一个状态s‘仍然是不确定的，这就成了影响target的唯一因素，所以说s’是自变量。正如上边所描述的，每次更新Q网络之后都会影响target的计算方法，这种target变化过于频繁的情况同样不利于学习的稳定性。所以我们单独设置独立于Q网络之外的target network，作为降低target计算方法变化的手段。target network是Q网络的一个复制版本，但是其的更新频率慢于Q网络，也就是Q网络更新若干次后才更新一次target network，这样就可以使得学习过程中Q网络有更多机会逼近target，取得更好的学习效果。这种想法就高度类似于supervised learning。更进一步来说，如果不设置target network，设想一个场景，一个状态s在进行动作a之后获得了一个奖励，进入下一个状态s‘。如果状态空间是平滑的（smooth），那么通常情况下相邻的两个状态的差别（参数上的）不会太大，也就是s与s'高度相似。在这个transition当中由于获得了奖励，当从replay buffer中选到这个transition进行训练时，就会试图增大这个(s, a)组合的Q函数值，但是由于Q网络的generalize特性，实际上与s非常相近的状态s‘相关的Q函数值也很可能会增大，这就导致了一个后果，当再次遇到这个状态的时候， 选择动作a会发现此时的target值更大了，而且和当前相比的距离和上次差不多，学习的结果就是进一步增大(s, a)。这个过程不断持续，最终造成的后果就是"chasing its own tail because of bootstrapping"，Q网络的某些位置可能会得出无穷的结果，导致学习失败。因此target network的设置是十分必要的。

DQN DQN的具体过程如左图所示，由于这个算法的重要性，在这里有必要对他的过程进行进一步的阐释。首先对replay buffer 进行初始化，注意D有大小限制N；然后对Q网络进行随机权重的初始化，并复制一份作为target网络的初始化。之后开始循环过程，每次循环的开头重新设定一个初始状态，随后进行T次的子循环处理，每次子循环中首先采用 策略进行action选择，确定状态-动作组合之后运行并获得奖励r和状态s‘，并将这个transition pair（s, a, r, s'）存入replay buffer。之后进行一次学习，在D中采样选出一定数量的transition作为minibatch进行学习，对选出的transition使用target network计算target值，之后采用误差函数计算误差，再进行梯度下降更新Q网络参数 。其中，每进行C次的Q网络更新，就进行一次target网络的更新，将最新版本的Q网络复制到target网络当中。

注意到在上边叙述DQN算法的过程时，并没有直接说使用方差的方法计算Q函数值和target的误差，这是因为我们通常选择采用别的误差函数例如Huber loss function，以其增强学习过程的鲁棒性。另外，神经网络训练的优化算法选择也会对Q网络的训练效果产生巨大的影响，实际上这也是deep reinforcement learning的一个特点，神经网络训练的优化算法会对训练效果产生很大影响，通常会使用 或 优化算法取代传统的 算法。另外， 算法中 算法的变化情况也应当加以注意，其的大小应该在第一阶段逐渐下降，在进行million量级次的训练过后，逐渐稳定在0.05到0.1左右的值。

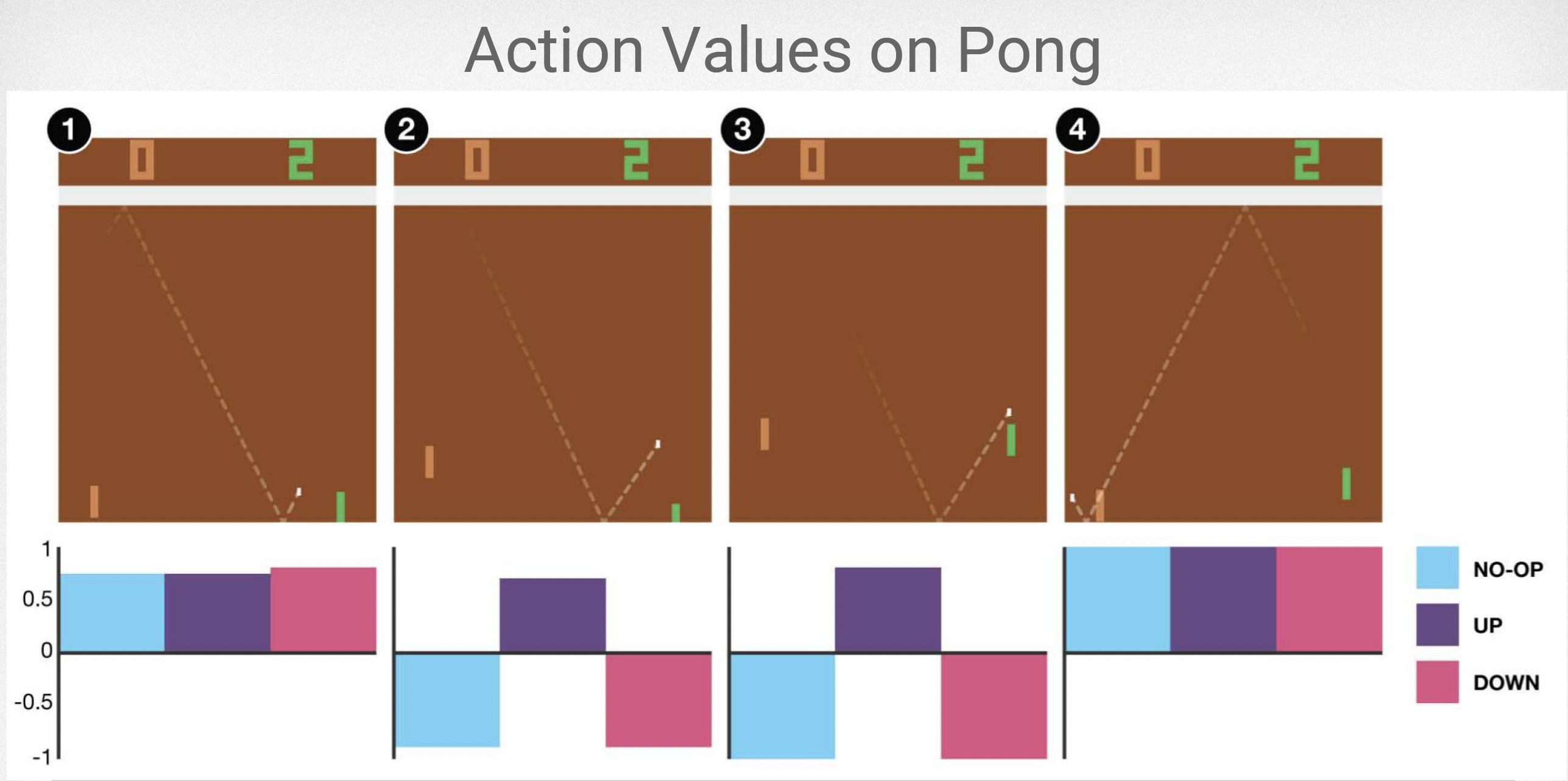pong 我们通常会使用Atari平台上的游戏来测试RL算法，结合CNN的方法，已经取得了很好的效果。正如左图展示的那样，我们在一个名为Pong的游戏当中测试算法性能，可以看到不同局面下Q网络给出的值，可选的动作有no-op，up，down三种，在1号局面下虽然小球距离右侧的距离已经很近，但是网络判定现在的局面还可以不用急于作出反应；2号局面和1号局面很相近，但是形势更加“危急”一点，Q网络判定此时“up”这一action的Q函数值是正的，而另外两个都是负的，说明Q网络希望引导agent作出向上移动的决定，这和我们的认知是符合的。另外两个局面也可以一样解读，Q网络的预测和我们的认知基本相似，其效果相当可观。

三、Double DQN以及一些其他的改进

这一部分列举了几个对于DQN的改进，首先要解释一点，作者之所以把Double DQN着重强调并不是由于它相比于别的改进版本更为重要，完全是出于个人需要，因为作者目前正在使用的TD3算法（基于policy gradient算法，是DDPG的改进版本）借鉴了Double DQN的思路，因此在这里着重提一下便于之后使用。

（1）Double DQN

在 当中我们给出了计算target的方法，其中采用max函数选择s‘状态下当前Q函数值最大的动作进行target计算。事实上这种方法存在估计值过大的偏向性(upward bias)，可能会导致最终Q网络的值偏高，影响正确决策。之前的DQN方法中采用target网络作为动作选择和评估的网络，也就是根据target网络Q函数值的大小评估s‘状态下各动作a’对应的(s', a')组合，选择最大的一个动作a‘【选择】，再直接使用刚刚用于评估的此a’的target网络Q值带入计算target【评估】。在double DQN算法中将选择和评估动作分开，选择时采用当前Q网络，评估的时候才采用target网络，即target计算是这样的

通过这种方式，可以有效减小upward bias，获得更好的学习效果

（2）Prioritized Experience Replay

在replay buffer中存储着相当数量的transition，但是在DQN算法当中，每次学习时都是针对其随机采样，没有任何偏向性，但是不同transition的“学习价值”是不同的，有的transition可能Q函数值和target值差距很小，学习价值较低；相应的差别较大的transition学习价值较高，值得反复学习，因此Prioritized Experience Replay采用Bellman error 来对transition赋予权重，使得采样时更有偏向性地选到值得反复学习的transition pairs，大大提高了学习效率。

（3）Dueling DQN

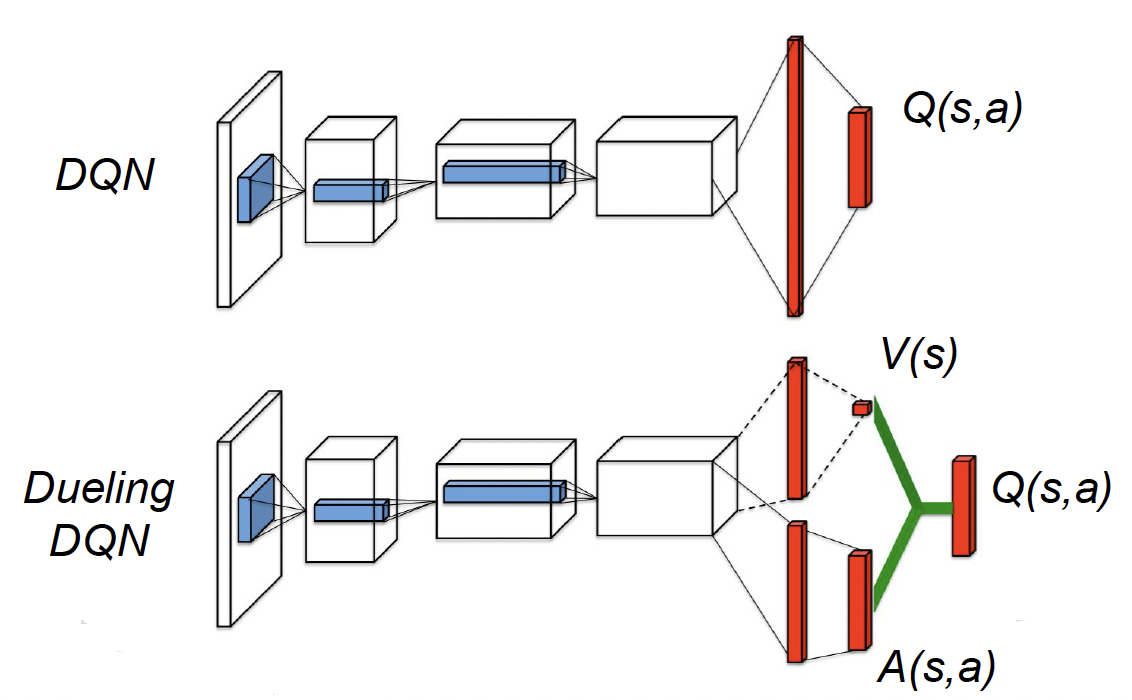dueling Dueling DQN将Q函数值进行分解，分解成value/advantege两个部分

正如上图所示，相比于传统DQN，Dueling DQN的Q函数网络输出的不是单一的Q(s, a)，而是V(s)和A(s, a)两部分，通过这种方法就可以奇迹般地提高学习效果。